Содержание
Входное сопротивление
Итак, имеем какой-либо блок. Как принято во всем мире, слева — это вход блока, справа — выход.
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение Uвх от другого блока или от источника питания, а на его выходе появится напряжение Uвых (или не появится, если блок является конечным).
Но раз уж мы подаем напряжение на вход (входное напряжение Uвх), следовательно, у нас этот блок будет кушать какую-то силу токаIвх.
Теперь самое интересное… От чего зависит Iвх ? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :
Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.
Выходное сопротивление
Яркий пример выходного сопротивления — это закон Ома для полной цепи, в котором есть так называемое «внутреннее сопротивление». Кому лень читать про этот закон, вкратце рассмотрим его здесь.
Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:
И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.
Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.
У всех аккумуляторов есть это внутреннее сопротивление r, и «цепляется» оно последовательно с источником ЭДС (Е).
Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.
В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (Eэквивалентное) и с каким-то внутренним сопротивлением (Rэквивалентное).
Eэкв — эквивалентный источник ЭДС
Rэкв — эквивалентное сопротивление
То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.
В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить Rвых ?
В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания Iкз.
В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что
Но есть небольшая загвоздка. Теоретически — формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.
Задачи для самостоятельного решения к главе vi
Задача 6.1. В схеме на рис. 6.1 найти выходное напряжение Uвых и ток в цепи обратной связи Iо.с для двух значений Er; Еr1=0.2B и Еr2=1В. Найти предельное значение Еr пр определяющее границу линейности схемы.
Задача 6.2 В схеме на рисунке 6.1 используется операционный усилитель со следующими данными: коэффициент усиления КОУ=50 10 3; входное сопротивление RвхОУ=1 мОм; выходное сопротивление
RвыхОУ=100 Ом. Параметры схемы: R0=5.1кОм; Rн=10 кОм. Найти усилительные параметры схемы – коэффициент усиления, входное и выходное сопротивления.
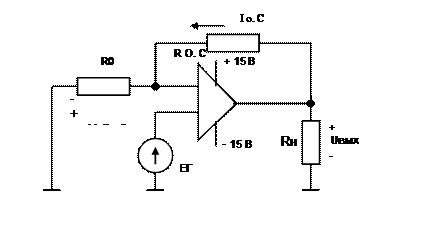
Рис.6.1.
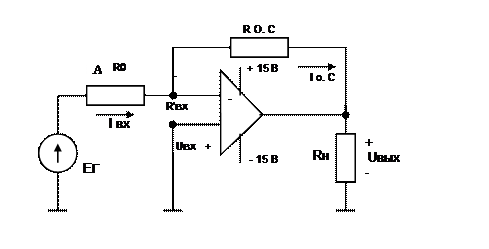
Рис.6.2.
Задача 6.3 В схеме на рисунке 6.2. ОУ имеет 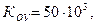


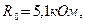
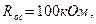
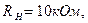 Найти коэффициент передачи усилителя, его входное и выходное сопротивления, сопротивление в точке А.
Найти коэффициент передачи усилителя, его входное и выходное сопротивления, сопротивление в точке А.
Рис.6.3.
Задача 6.4. В схеме на рис.6.3. 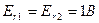
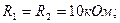
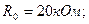
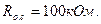 Чему равны напряжения на инвертирующем входе Uпх и выходе Uвых? Чему равен ток в цепи обратной связи
Чему равны напряжения на инвертирующем входе Uпх и выходе Uвых? Чему равен ток в цепи обратной связи  ? Считать операционный усилитель идеальным.
? Считать операционный усилитель идеальным.
Подсказка. 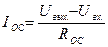
Задача 6.5. В схеме на рис.6.4. Еr1=1В; Еr2 = -2В; R1=10 kOм; R2=20 кОм. Определитель напряжение на выходе Uвых и ток в цепи обратной связи Io.с. Как изменится ток Io.с, если сопротивление Ro.с увеличится в двое?

Задача 6.6. Дополните схему (рис.6.1.) такими элементами, чтобы получить неинвертирующий повторитель. Докажите, что 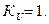
Примеры решения задач
Примеры решения задач к главе I
Задача 1.2. Транзистор с коэффициентом передачи тока базы b=49 используется в схеме на рис. 1.5. Определить напряжения UБЭ и UКЭ при Т=50°С, если при Т=20°С обратные токи коллекторного и эмиттерного переходов одинаковы и равны 10 мкА, а температура удвоения обратного тока равна 10°С.
Решение. Используя подсказку, приведенную в задаче 1.2. к главе I, вычислим сначала значения токов эмиттера и напряжения на коллекторном переходе в схеме при начальной температуре Т=20°С. Базовый ток для схемы, приведенной на рисунке 1.5. задается источником напряжения ЕК и резистором в цепи базы RБ и будет равен
IБ » ЕК / RБ = 20 / (200 · 103) = 0,1 мА
Вычислим эмиттерный ток по формуле
IЭ = (1 b)(IБ IК 0)
Получим, что IЭ = (1 49)(0,1 0,01) ´ 10-3 = 5,5 мА.
Вычислим напряжение на эмиттерном переходе транзистора:
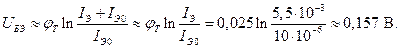
Вычислим ток коллектора по формуле IК = bIБ IК 0 (1 b) и получим
IК = 49 · 0,1 · 10-3 10-5 · 50 = 5,4 мА.
Вычислим напряжение коллектор-эмиттер по формуле UКЭ = ЕК – IKRK
и получим:
UКЭ = ЕК – IKRK = 20 – 5,4 · 2 = 9,2 В.
Проведем аналогичные вычисления для конечной температуры Т = 50°С. Учитывая, что при увеличении температуры увеличиваются обратные токи переходов, воспользуемся следующей формулой IK0(T2) = IЭ0(T2) = I0(T1)2∆Т/Ту.
Где ∆Т = Т2 – Т1 = 50 – 20 = 30°С; Ту = 10°С – температура удвоения; I0(T1) – значение теплового тока через переход при Т1.
Подставив значения в формулу, получим значение обратного тока при новой температуре :
I0(50°С) = 10-5 · 230 / 10 = 80 мкА.
Вычислим значение температурного потенциала jТ
jТ = Т / 11600 = 323 / 11600 » 0,028 В.
Вычислим падение напряжения на эмиттерном переходе
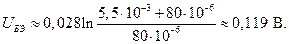
Видим, что напряжение на эмиттерном переходе уменьшилось. А значение тока коллектора будет равно
IК = 4,9 · 10-3 80 · 10-6 · 50 = 8,9 мА.
С ростом коллекторного тока напряжение на участке коллектор-эмиттер уменьшается и будет равно
UКЭ = 20 – 8,9 · 2 = 2,2 В.
Задача 1.4. В схеме, приведенной на рис.1.4 а, транзистор имеет 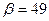 . Найти постоянное напряжение на коллекторе транзистора
. Найти постоянное напряжение на коллекторе транзистора  , если
, если 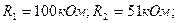
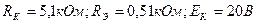
Решение. Первым шагом попытаемся преобразовать схему к более удобному виду (см. на рис.1.4 б.) Из полученной схемы получим, что
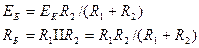


Чтобы найти постоянное напряжение на коллекторе транзистора, воспользуемся формулой 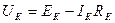 .
.
Ток коллектора находим по формуле 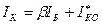 , ток базы – по формуле, через вычисление
, ток базы – по формуле, через вычисление 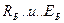 . Произведем вычисления :
. Произведем вычисления :

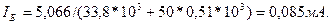
Итак, получили, что постоянное напряжение на базе транзистора равно:

А ток коллектора равен:
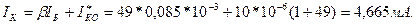
Получили, что постоянное напряжение на коллекторе равно:
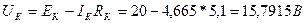 .
.
Примеры решения задач к главе II
Задача 2.1. В каскаде ОЭ (рис. 2.11) используется транзистор, у которого h11Э=800 Ом; h12Э=5·10-4; h21Э=49; h22Э=80 мкСм. Найти коэффициенты усиления по напряжению и по току, входное и выходное сопротивления, если
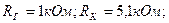
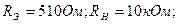 Решить задачу с учетом и без учета
Решить задачу с учетом и без учета 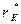 .
.
Решение. Для решения задачи воспользуемся следующими соотношениями:
KU = — bRКн / (Rг Rвх), RКн = RК || Rн = RКRн / (RК Rн), Rвых = RК || 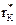 (1 bgБ), gБ = RЭ / (RЭ Rг), Rвх = rБ (rЭ RЭ)(1 h21Э) = rБ rЭ(1 h21Э) RЭ(1 h21Э), rБ rЭ(1 h21Э)= h11Э.
(1 bgБ), gБ = RЭ / (RЭ Rг), Rвх = rБ (rЭ RЭ)(1 h21Э) = rБ rЭ(1 h21Э) RЭ(1 h21Э), rБ rЭ(1 h21Э)= h11Э.
Вычислим Rвх = h11Э (1 h21Э) RЭ.
Подставим параметры, приведенные в условии задачи и получим, что
Rвх = 800 49 · 0,51 · 103 = 25,8 кОм.
Найдем выходное сопротивление
Rвых = RК || 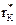 (1 bgБ),
(1 bgБ),
где gБ = RЭ / (RЭ Rг) – коэффициент токораспределения в базе транзистора; 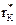 =1/h22Э – дифференциальное сопротивление коллекторного перехода.
=1/h22Э – дифференциальное сопротивление коллекторного перехода.
Подставим данные:
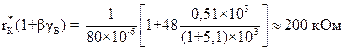 .
.
Окончательно имеем, что
Rвых = 5,1 · 103 || 200 · 103 = 5,1 · 200 / (5,1 200) · 103 » 4,9 кОм;
Rвых » RК .
Вычислим коэффициент передачи по напряжению KU = — bRКн / (Rг Rвх)=
где b»h21Э – коэффициент передачи тока базы; RКн = RК || Rн = RКRн / (RК Rн) – эквивалентное сопротивление в цепи коллектора.
Получим, что
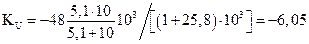 . Знак минус говорит об инверсии сигнала.
. Знак минус говорит об инверсии сигнала.
Рассчитаем коэффициент усиления по току
 .
.
Задача 2.2. Найти усилительные параметры каскада, показанного на рис. 2.11, если он нагружен на аналогичный каскад.
Решение. В качестве нагрузки усилительного каскада следует рассматривать входное сопротивление второго каскада. Из решения задачи 2.1 имеем, что
Rн = Rвх2 .
Рассчитаем коэффициенты усиления по току и напряжению, воспользовавшись вышеприведенными формулами. Получим, что:
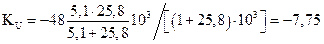 ;
;
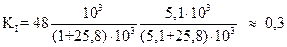 .
.
Задача 2.3. Найти коэффициент усиления КU и верхнюю граничную частоту усилителя ОЭ (рис 2.14), в котором использован транзистор со следующими параметрами: b = 49; fh21Э = 5 МГц; rЭ = 25 Ом; rБ = 150 Ом;  =30 кОм; СК = 5 пФ. Номиналы резисторов и рис. взять из задачи 2.1..
=30 кОм; СК = 5 пФ. Номиналы резисторов и рис. взять из задачи 2.1..
Решение. Воспользуемся определением верхней граничной частоты усилителя ОЭ. Знаем, что она может вычисляется через постоянную времени в области верхних частот:
fв = 1 / (2ptв) ; tв = (tb tК) / (1 — bgБ) ,
здесь gБ = (rЭ RЭ) / (Rг rБ rЭ RЭ) – коэффициент токораспределения в цепи базы, tb = 1 / wb = 1 / (2p fh21Э) — постоянная времени коэффициента передачи тока базы; tК =  (
( 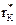 ||RКн) – постоянная времени коллекторной цепи.
||RКн) – постоянная времени коллекторной цепи.
Вычислим tК = 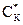 (
( 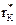 ||RКн) .
||RКн) .
Здесь RКн = (RК Rн) / (RК Rн) = (3 · 10) / (3 10) · 103 » 2,3 кОм, так как 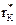 >> RКн , то tК »
>> RКн , то tК » 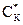 RКн = СК (1 b) RКн = 5 · 10-12 · 50 · 2,3 · 103 » 0,58 · 10-6 с.
RКн = СК (1 b) RКн = 5 · 10-12 · 50 · 2,3 · 103 » 0,58 · 10-6 с.
tb = 1 / (2 p fh21Э) = 1 / (2 · 3,14 · 100 · 103) » 1,6 · 10-6 с.
gБ = (25 510) / (103 150 25 510) = 0,31.
tв = (1,6 0,58) · 10-6 / (1 49 · 0,31) » 0,13 · 10-6 с.
Найдем верхнюю граничную частоту усилителя
fв = 1 / (2ptв) = 1 / (2 · 3,14 · 0,13 · 10-6) » 1,22 · 106 Гц.
Вычислим коэффициент усиления по напряжению КU по формуле
КU = — bRКн / ( Rг Rвх) = — (49 · 2,3 · 103) / [103 150 (25 510)(1 49)] =
= — 4,11.
Знак минус говорит об инверсии фазы.
Задача 2.6. Для условий, сформулированных в задаче 2.1. определить, в каких пределах изменяется выходное сопротивление каскада при изменении Rвх от нуля до бесконечности.
Решение. Воспользуемся следующим выражением: 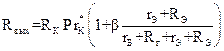 .
.
Мы знаем, что rЭ, rБ и RЭ являются составными элементами входного сопротивления каскада. При Rвх ® ¥, формула принимает следующий вид :
Rвых = RК || 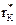 (1 b) = RК ||rК .
(1 b) = RК ||rК .
При Rвх ® 0 получим, что Rвых » RК || 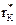 . При данных условиях видно, что выходное сопротивление каскада при изменении Rвх от нуля до бесконечности
. При данных условиях видно, что выходное сопротивление каскада при изменении Rвх от нуля до бесконечности
приближается к RК, но при Rвх ® ¥ это приближение точнее.
Примеры решения задач к главе III
Задача 3.5. На рис. 3.5. представлен усилительный каскад с общим истоком (ОИ) на полевом транзисторе с р-п переходом. Определить усилительные параметры этой схемы, если крутизна стокозатворной характеристики S = 10 мА / В. Считаем, что S выражается в мА / В, а R в кОм.
Решение. Для определения усилительных параметров каскада применим формулу KU = SRСн / (1 SRИ), которая справедлива, когда резистор RИ не зашунтирован блокировочным конденсатором. Воспользуемся формулами для определения входноего и выходного сопротивлениея схемы с общим истоком
Rвх = RЗ || [(RвхИТ RИ)(1 SRИ)] , а также формулой для определения эквивалентного сопротивления в цепи стока RСн = RС || Rн.
Здесь RвхИТ – входное сопротивление полевого транзистора, достигающее на практике 108 – 109 Ом. Поскольку RЗ << RвхИТ , можно записать
Rвх » RЗ = 560 кОм.
Итак, коэффициент усиления равен:
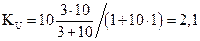 .
.
Найдем выходное сопротивление схемы ОИ:
Rвых = RС || rС ,
Здесь rС – дифференциальное сопротивление канала. Т.к. rС достаточно велико и учитывая параллельное включение, можно считать, что Rвых » RС .
Задача 3.6. В схеме истокового повторителя на полевом транзисторе с р-п переходом (рис. 3.6.) использован транзистор с крутизной стокозатворной характеристики 12 мА / В. Определить усилительные параметры истокового повторителя.
Решение. Определим усилительные параметры каскада, используя следующие формулы: KU = [SUЗИ (RИ || Rн)] / [UЗИ SUЗИ (RИ || Rн)] = S (RИ || Rн) / [1 S(RИ || Rн)], Rвх » RЗ, Rвых = RИ / (1 SRИ), RИ || Rн = (2 · 0,1) / (2 0,1) = 0,095 кОм;
Проведя соответствующие подстановки, получим, что :
KU = (12 · 0,095) / (1 12 · 0,095) » 0,53 .
Входное сопротивление истокового повторителя равно
Rвх » RЗ = 0,2 МОм.
Найдем выходное сопротивление:
Rвых = RИ / (1 SRИ) = 3 / (1 12 · 3) = 0,081 кОм.
Задача 3.7. Для схемы, описанной в задаче 3.3, найти усилительные параметры каскада, когда нагрузкой схемы служит аналогичный каскад.
Решение. Из условия задачи имеем, что Rн » Rвх = 26 Ом.
Найдем коэффициенты передачи по току и напряжению KU и KI:
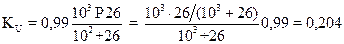 ;
;
 .
.
Задача 3.8. Определить верхнюю граничную частоту каскада ОБ (рис. 3.4.), в котором использован транзистор со параметрами: a = 0,98; fh21Б = 10 МГц; rЭ = 25 Ом; rБ = 150 Ом; rК = 1,5 МОм; СК = 5 пФ? Элементы: Rг = 50 Ом; RЭ = 6,2 кОм; RК = 2 кОм; Rн = 5 кОм.
Решение. Воспользуемся формулами: fв = 1 / (2ptв), где fв — верхняя граничная частота схемы ОБ, tв— постоянная времени в области верхних частот.
Знаем, что в схеме с ОБ транзистор реализует свои частотные свойства максимально. Верхняя граничная частота усилителя ОБ имеет пределом граничную частоту коэффициента передачи эмиттерного тока fa » fh21Б . Другим важным фактором, снижающим быстродействие транзистора, является СК — емкость коллекторного перехода ; tв = (ta tК) / (1 — agЭ) ,
где ta — постоянная времени коэффициента передачи a; tК = СК (RКн || rК) – постоянная времени цепи коллектора; gЭ = rБ / (rБ Rг rЭ) – коэффициент токораспределения в цепи эмиттера.
Найдем коэффициент токораспределения
gЭ = 150 / (150 50 25) » 0,67.
Посчитаем костоянная времени коллекторной цепи
tК = СК (RКн || rК) » СК RКн ;
RКн = RК || Rн = (2000 · 5000) / (2000 5000) = 1,43 · 103 Ом;
tК = 5 · 10-12 · 1,43 · 103 = 7,15 · 10-9 = 7,15 мс.
Постоянная времени коэффициента передачи a
ta = 1 / (2 p fh21Б) = 1 / (2 · 3,14 · 10 · 106) = 16,42 · 10-9 с.
Постоянная времени усилителя в области верхних частот
tв = (16,42 7,14) · 10-9 / (1 – 0,98 · 0,67) = 78,5 · 10-9 с.
Найдем верхнюю граничную частоту усилителя:
fв = 1 / (1 · 3,14 · 78,5 · 10-9) = 4,5 · 106 .
Задача 3.9. Решить задачу 3.5. для случая, когда нагрузкой является аналогичный каскад.
Решение. Нагрузкой в схеме на рис. 3.5. является входное сопротивление аналогичного каскада, составляющее сотни килоом, поэтому можно считать, что RС << Rн . Решим задачу и получим, что:
RСн = RС || Rн » RС ;
KU = SRС / (1 SRИ) = 10·3 / (1 10 · 1)  .
.
Задача 3.10. Определить коэффициент усиления схемы, представленной на рис. 3.5. если, отсутствует резистор RИ.
Решение. Так как RИ = 0 , то выражение для определения коэффициента усиления каскада примет вид, что :
KU = SRСн .
Подставив значения, получим что :
KU = SRС = 10·3 = 30.
Примеры решения задач к главе IV
Задача 4.2. На рис. 4.1. предоставлена схема с эмиттерной связью. Найти напряжение выходного сигнала, если транзисторы идентичны и имеют следующие параметры: b = 100; rЭ = 100 Ом; rБ = 200 Ом; 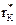 =30 кОм. Входные напряжения: Uвх1 = 1 В, а Uвх2 = 1,1 В.
=30 кОм. Входные напряжения: Uвх1 = 1 В, а Uвх2 = 1,1 В.
Решение: Используя подсказку, приведенную в условии задачи к главе IV, применим принцип суперпозиции и получим, что
Uвых = Uвх1 K1 Uвх2 K2 .
Здесь
K1 = Uвых / Uвх1 |Uвх2=0 ; K2 = Uвых / Uвх2 |Uвх1=0 .
Относительно сигнала Uвх2 схема является усилителем ОЭ.
K2 » – RК / rЭ = -30 .
По отношению к сигналу Uвх1 усилитель является двухкаскадной схемой ОК–ОБ. Тогда справедливо соотношение K1 = КUОК KUОБ .
Здесь КUОК = (1 b)( RЭ || rЭ) / [rБ ( RЭ || rЭ) (1 b)] » 1, КUОБ = aRК / Rвх ОБ » aRК / rЭ .
Будем считать, что a » 1, тогда имеем, что КUОБ » RК / rЭ = (3 · 103) / 100 = 30.
Получим, что коэффициент усиления для Uвх1 будет равен
K1 = 1 · 30 = 30.
Из решения следует, что К1 = К2 , т.е. коэффициенты усиления сигналов Uвх1 и Uвх2 равны, но Uвх2 инвертируется, а Uвх1 нет.
Амплитуда сигнала на выходе схемы с эмиттерной связью равна:
Uвых = 1,0 · 30 1,1 · (-30) = — 3 В.
Задача 4.3. На рисунке 4.2. предоставлен каскодный усилитель. Транзисторы Т1 и Т2 идентичны и имеют параметры: b = 49; rЭ = 10 Ом; rБ = 80 Ом; rК = 1 Мом. Другие элементы схемы: Rг = 10 кОм; RК = 5,1 кОм; Rн = 10 кОм; RЭ = 200 Ом. Определить усилительные параметры схемы: KU, KI и KР .
Решение. Для расчета применим следующие формулы: Rвх = rБ (rЭ RЭ)(1 b) ; КР = KU KI; 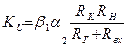 ;
; 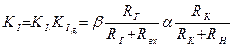 .
.
Входное сопротивление схемы равно:
Rвх = 80 (10 200)(1 49) = 10,58 кОм.
Коэффициент усиления по току

Найдем коэффициент усиления по напряжению каскодного усилителя как усиление составного транзистора Т1 – Т2 :
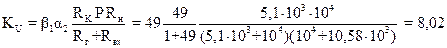 .
.
Вычислим коэффициент усиления по мощности:
КР = KU KI = 8,02 · 1,37 = 10,99.
Задача 4.5. Для каскодной схемы, приведенной на рис. 4.3., а обеспечить коэффициент усиления по напряжению 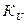 =4
=4 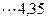 в диапазоне рабочих частот от нуля до 10 МГц. Считать транзисторы однотипные со следующими параметрами: a = 0,99; rЭ = 20 Ом; rБ = 120 Ом; rК = 2 МОм; fa = 200 МГц; СК = 1 пФ?
в диапазоне рабочих частот от нуля до 10 МГц. Считать транзисторы однотипные со следующими параметрами: a = 0,99; rЭ = 20 Ом; rБ = 120 Ом; rК = 2 МОм; fa = 200 МГц; СК = 1 пФ?
Решение. Используя формулы КU0 = — (abRКн) / ( Rг Rвх), где Rвх = rБ (rЭ RЭ)(1 b), рассчитаем коэффициент усиления по напряжению для низких и средних частот.
b = a / (1 — a) = 0,99 / (1 – 0,99) = 99;
Rвх = 120 (20 103)(1 99) = 102,12 · 103 Ом;
RКн = RК || Rн = (10 · 10) / (10 10) · 103 = 5 кОм;
КU0 = — (0,99 · 99 · 5 · 103) / (103 102,12 · 103) » — 4,75.
Определим постоянная времени каскада ОБ на транзисторе Т2 :
tв ОБ = (ta tК) / (1 — agЭ) ;
ta = 1 / (2 p fa) = 1 / (2 · 3,14 · 200 · 106) = 0,796 · 10-9 с;
tК = СК RКн = 10-12 · 5 · 103 = 5 · 10-9 с;
gЭ = (rБ RБ) / (rЭ rК rБ RБ) » RБ / (rК RБ) = 105 / (2 · 106 105) = 0,0476;
tв ОБ = (0,796 5) · 10-9 / (1 – 0,99 · 0,0476) = 6,05 · 10-9 с.
Определим постоянную времени каскада ОЭ на первом транзисторе Т1 :
tв ОЭ = (tb tК) / (1 — bgБ) ;
tb = ta (1 b) = (1 b) / (2 p fa) = (1 99) / (2 · 3,14 · 200 · 106) » 3,18 · 10-6 с;
tК = 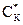 Rвх ОБ =
Rвх ОБ = 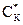 [rЭ (rБ RБ) / (1 b)] = 10-12 · 100[20 (120 105) / (1 99)] = 1,02 · 10-7 с;
[rЭ (rБ RБ) / (1 b)] = 10-12 · 100[20 (120 105) / (1 99)] = 1,02 · 10-7 с;
gБ = (rЭ RЭ) / (Rг rБ rЭ RЭ) = (20 103) / (103 120 20 103) » 0,48;
tв ОЭ = (0,08 0,102) · 10-6 / (1 99 · 0,48) » 3,75 · 10-9 с.
Определим эквивалентную постоянную времени усилителя в области верхних частот
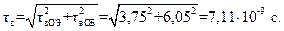
Определим коэффициент усиления каскодного усилителя на частоте 10 МГц:
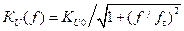 ,
,
Здесь fв – верхняя граничная частота усилителя и равна fв = 1 / (2ptв) = 1 / (2 · 3,14 · 7,11 · 10-9) = 22,4 · 106 Гц.
Тогда для коэффициент усиления каскодного усилителя на частоте 10 МГц получаем, что 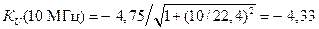 .
.
Примеры решения задач к главе V
Задача 5.1. На рис. 5.1. представлена схема дифференциального усилителя. Транзисторы идентичны и имеют следующие параметры: b = 100; rЭ = 100 Ом. Чему равно напряжение на нагрузке Rн , если Uвх1 = 1 В, а Uвх2 = 1,1 В?
Решение. 1. Выражение для вычисления сигнала на выходе дифференциального усилителя имеет вид Uвых = Kд ∆U = Kд (Uвх2 – Uвх1) и прямо пропорционален разностному значению входных напряжений, которое определяется как дифференциальный сигнал:
Здесь 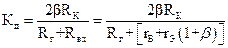 – коэффициент усиления дифференциального сигнала.
– коэффициент усиления дифференциального сигнала.
Для интегральных схем, работающих в микрорежиме, характерно высокое сопротивления rЭ. В следствии этого формулу для определения коэффициента усиления дифференциального сигнала можно преобразовать и считать, что:
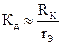 .
.
Найдем Кд : 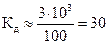 .
.
Значение сигнала на выходе дифференциального усилителя будет равно
Uвых д = 30 (1,1 – 1,0) = 3 В.
К появлению выходной синфазной ошибки может привести наличие двух совпадающих по фазе (синфазных) сигналов . Эта ошибка обусловлена приращениями токов в коллекторных цепях транзисторов Т1 и Т2:
Uвых = Uвх. с Kс2 – Uвх. с Kс1 = Uвх. с (Kс2 – Kс1) ,
где Uвх. с равно меньшему из двух входных сигналов.
Коэффициент усиления синфазного сигнала для каждого из плеч дифференциального усилителя определяется следующим выражением:
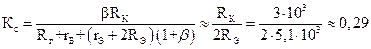 .
.
В случае идентичности плеч (что соответствует условию задачи) коэффициенты усиления синфазных сигналов в обоих плечах одинаковы, и, следовательно. в нашем случае выходная синфазная ошибка равно нулю.
Задача 5.3. Чему равно напряжение на выходе дифференциального усилителя при значениях входных сигналов Uвх 1= 1В, Uвх 2 = 1,1В при условии, что плечи дифференциального усилителя, в схеме, показанной на рис. 5.1., неидентичны: RК1 = 3 кОм, RК2 = 3,1 кОм.
Решение. Воспользуемся выражением для вычисления коэффициента усиления дифференциального сигнала в случае разности номиналов резисторов. 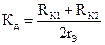 ,
,
здесь в качестве коллекторного резистора следует брать среднее значение RК1 и RК2 .
Напряжение на выходе дифференциального усилителя без учета выходной синфазной ошибки будет равно:
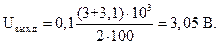
В отличие от только что рассмотренной задачи 5.1. для дифференциального усилителя с идентичными плечами выходное дифференциальное напряжение усилителя задачи 5.3. отличается на 0,05 В. Величину этой разности будем рассматривать как выходную дифференциальную ошибку, обусловленную асимметрией плеч.
Посчитаем выходную синфазную ошибку на выходе дифференциального усилителя :
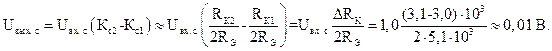
Посчитаем суммарное выходное напряжение дифференциального усилителя. Оно составит 3,05 0,01=3,06 В. Синфазную ошибку можно уменьшить, увеличивая RЭ . Ясно, что при RЭ ® ¥ синфазная ошибка стремится к нулю.
Примеры решения задач к главе VI
Задача 6.4. В схеме на рис. 6.3. 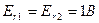
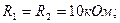
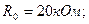
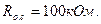 Определить значения напряжений на инвертирующем входе Uпх и выходе Uвых. Чему равен ток в цепи обратной связи
Определить значения напряжений на инвертирующем входе Uпх и выходе Uвых. Чему равен ток в цепи обратной связи  ? При условии, что операционный усилитель идеальный.
? При условии, что операционный усилитель идеальный.
Решение. Рассмотрим схему. Это — неинвертирующий сумматор. Сумма токов, отбираемых от источников 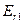 и
и 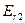 , равна нулю, так как неинвертирующий вход тока не потребляет. Можно записать, что
, равна нулю, так как неинвертирующий вход тока не потребляет. Можно записать, что
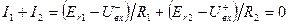
Так как в данной схеме выполняется условие равенства напряжений 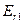 и
и 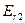 и сопротивлений R1 и R2, то от источников отбираются одинаковые токи I 1 и I2. Такое возможно только лишь при выполнении условия, что I1=I2=0, или
и сопротивлений R1 и R2, то от источников отбираются одинаковые токи I 1 и I2. Такое возможно только лишь при выполнении условия, что I1=I2=0, или 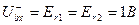 .
.
Так как операционный усилитель находится в линейном режиме, то напряжение 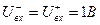 .
.
Вычислим напряжение на выходе и ток в цепи обратной связи неинвертирующего сумматора :
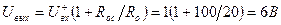
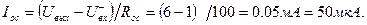
Задача 6.5. В схеме на рис. 6.4. Еr1=1В; Еr2 = -2В; R1=10 kOм; R2=20 кОм. Определитель напряжение на выходе Uвых и ток в цепи обратной связи Io.с. Как изменится ток Io.с, если сопротивление Ro.с увеличится в двое?
Решение. Схема на рисунке 6.4. представляет собой инвертирующий сумматор с разными масштабными коэффициентами слагаемых напряжений. Определим напряжение на выходе Uвых и ток в цепи обратной связи Io.с.
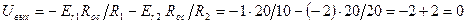
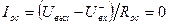 Из результата проведенных вычислений видно, что при увеличении Rо.с ток в цепи обратной связи Iо.с останется равным 0.
Из результата проведенных вычислений видно, что при увеличении Rо.с ток в цепи обратной связи Iо.с останется равным 0.
Задача 6.7. В схеме, приведенной на рисунке 6.1. используется операционный усилитель со следующими данными: коэффициент усиления КОУ=50 10 3; входное сопротивление RвхОУ=1 мОм; выходное сопротивление —
RвыхОУ=100 Ом. Параметры схемы: R0=5.1кОм; Rн=10 кОм. Найти усилительные параметры схемы – коэффициент усиления, входное и выходное сопротивления.
Решение. Приведенная на рисунке 6.1. схема называется неинвертирующим усилителем. В данной схеме используется последовательная отрицательная обратная связь по напряжению, так как напряжение обратной связи U0C пропорциональное входному напряжению связи Uвых включено встречно усиливаемому сигналу Еr.
Вычислим входное сопротивление для схемы с ПООС по напряжению по формуле: 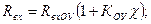
здесь 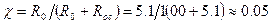 МОм
МОм
Итак, получили : 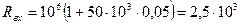 Мом.
Мом.
Определим выходное сопротивление усилителя :
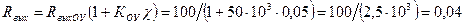 Ом
Ом
Так как сопротивление Rн=10 кОм значительно больше выходного сопротивления схемы, оно на расчет не влияет.
Вычислим коэффициент усиления усилителя по формуле :
 .
.
Задача 6.8. В схеме на рис. 6.1. найти предельное значение Еr пр ,определяющее границу линейности схемы, выходное напряжение Uвых и ток в цепи обратной связи Iо.с для двух значений Er; Еr1=0.2B и Еr2=1В.
Решение: Найдем значения Uвых и Iо.с по формулам :
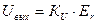 ;
; 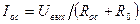 ;
;
Здесь следует обратить внимание на то, что входное сопротивление операционного усилителя со стороны инвертирующего входа велико и сопротивление R0 им не шунтируется.
Если Er= Еrß=0,2 В, то  В, и ток в цепи обратной связи Iо.с и равен :
В, и ток в цепи обратной связи Iо.с и равен :
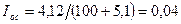 мА.
мА.
Если выполняется условие : Er= Еr2 =1В , то, казалось бы, что 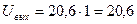 В. Но мы знаем, что Uвых не может быть больше чем Uвых=14 В , что на 1 В по абсолютной величине меньше значения напряжения питания Er = 15В или E2=-15В
В. Но мы знаем, что Uвых не может быть больше чем Uвых=14 В , что на 1 В по абсолютной величине меньше значения напряжения питания Er = 15В или E2=-15В
Следовательно, в этом случае Uвых= -14 В. И тогда ток в цепи обратной связи Iо.с
равен :  В.
В.
Найдем предельное значение Еr пр ,определяющее границу линейности схемы,  .
.
Тема «Основы схемотехники»
Физический факультет
Кафедра радиофизики
Авторы: Артемов К.С.
Солдатова Н.Л.
Приложение №1
Измерение входного сопротивления на практике
Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:
А на деле вот так:
Итак, у нас получилось 22,5 миллиАмпер.
Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:
Получаем:
Измерение выходного сопротивления на практике
Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R.
Итак, для начала замеряем напряжение на аккумуляторе без лампочки.
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер.
Как измерить входное сопротивление
Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?
1)Замерить напряжение Uвх, подаваемое на этот блок
2)Замерить силу тока Iвх, которую потребляет наш блок
3) По закону Ома найти входное сопротивление Rвх.
Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.
Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).
Падение напряжения на резисторе R обозначим, как UR
Из всего этого получаем…
Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!
Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление Rвх=1МегаОм, а резистор взяли R=1 КилоОм.
Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.
В результате получается цепь:
Высчитываем силу тока в цепи в Амперах
Получается, что падение напряжения на сопротивлении R в Вольтах будет:
Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.
Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.
Предисловие
Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие «блок». Например, источник питания, собранный по этой схеме:
состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.
В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:
Блочная схема — это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку.
Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.
— Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?
Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.
На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.
Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением.
Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление — это сопротивление какого-то входа, а выходное — сопротивление какого-либо выхода. Ну да, все почти так и есть.
Примеры задач до темы лекции 8
Вопросы для самопроверки
1. Почему коэффициент усиления ФИК с разделенной нагрузкой меньше единицы ?
2. Какие достоинства ФИК с эмиттерной связью ?
3. Нарисуйте схему фазоинверсного каскада с разделённой нагрузкой и поясните принцип работы.
4. Нарисуйте схему фазоинверсного каскада на двух транзисторах с общим эмиттером.
5. Нарисуйте схемы эмиттерных повторителей и поясните принцип их работы.
6 Перечислите достоинства плавной потенциометрической регулировки
усиления
7 Назовите недостатки плавной потенциометрической регулировки
усиления.
8 Что называют глубиной регулировки усиления ?
9 В каких случаях используют потенциометрическую регулировку
последовательным переменным резистором, и в каких – параллельным ?
Задача 1
В схеме истокового повторителя на полевом транзисторе с р-п переходом ( рисунок 1.54 ) использован транзистор с крутизной стокозатворной характеристики 12 мА / В. Величина резистора R1=2 МОм,
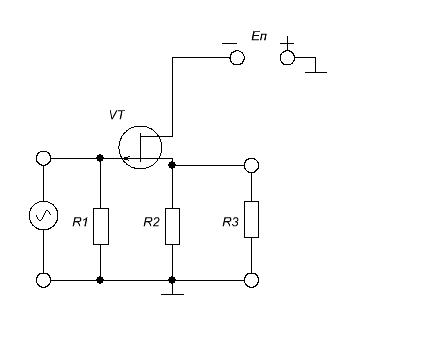 R2= 2кОм, R3= 100 Ом. Определить усилительные параметры истокового повторителя.
R2= 2кОм, R3= 100 Ом. Определить усилительные параметры истокового повторителя.
Рисунок 1.54 — Схема истокового повторителя
Решение : Для истокового повторителя из усилительных параметров имеют смысл коэффициент передачи по напряжению, входное и выходное сопротивления.
1 Коэффициент передачи по напряжению
Кu = [SUзи( Rи//Rн)]/[Uзи SUзи(Rи//Rн)] =
S(Rи//Rн)/[1 S(Rи//Rн)].
Подставим крутизну в миллиамперах на вольт, а сопротивление – в килооммах, вычислив предварительно эквивалентное сопротивление в цепи истока:
Rи//Rн = ( 2 0,1) / (2 0,1 ) = 0,095 кОм ,
Кu = ( 12 0,095) / ( 1 12 0,095) ≈ 0,53
2 Входное сопротивление истокового повторителя
Rвх≈R1 = 2 М Ом,
3 Выходное сопротивление
Rвых = Rи/ ( 1 SRи ),
Rвых = 3 /( 1 12 3) = 0,081 кОм.
Близкий результат дает упрощенная формула
Rвых≈ 1 / S,
Rвых≈ 1/12 ≈ 0,083 кОм.
Задача 2
Определить выходное напряжение в схеме эмиттерного повторителя
( рисунок 1.55) при Uвх=0, если падения напряжения на открытом эмиттерном переходе в режиме R1 равны Uбэ = 0,6 В, UR1 = 5,4 В. Напряжение источника питания Ек = 10 В.
Решение : Выходное напряжение в схеме эмиттера повторителя равно
Uвых = Uэ = Ек — Uбэ — UR ,
Uвых = 10 – 0,6 – 5,4 = 4 В
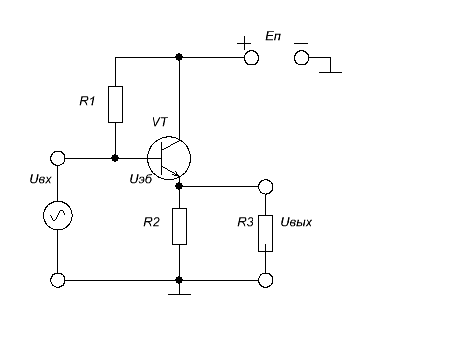
Рисунок 1.55 — Схема эмиттерного повторителя
Задача 3
Определить сопротивление резистора R1 в базовой цепи транзистора, при котором на выходе схемы эмиттерного повторителя ( рисунок 1.55) при
Uвх =0 создается напряжение Uвых = Uэ = 5 В. Сопротивление резистора R2 = 1 кОм. Напряжение источника питания Ек = 12 В. падение напряжения Uбэ=0,6 В. Коэффициент усиления транзистора по току h21э=50.
Решение :
1 Падение напряжения на резисторе R1
Ек = UR1 Uбэ Uэ ,
UR1 = Ек — Uбэ — Uэ ,
UR1 = 12 – 0,6 — 5 = 6,4 В
2 Ток базы транзистора Iб равен
Uэ =IэRэ = Iб ( h21э 1 ) R2 ,
Iб = Uэ /( h21э 1 ) R2 ,
Iб = 5 / ( 50 1)1 103 =0,1 10-3,
3 Величина резистора R1 равна
UR1 = Iб R1 ,
R1 = UR1 / Iб ,
R1 = 6,4 / 0,1 10 -3 = 64 кОм
Решение
Как следует из рис. 4.17,
I1 I2=-IC,
или
U1-UиR1 U2-UиR2=-CdUвыхdt.
Следовательно для идеального операционного усилителя
Uвых=-1R1∙C0tU1dt-1R2∙C0tU2dt,
Uвых=-1200∙103∙0,82∙10-60600,1dt-1100∙103∙0,82∙10-6060-0,05dt;
Uвых=-1200∙103∙0,82∙10-6060,1dt-1100∙103∙0,82∙10-606-0,05dt.
Заключение
Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.
С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе.
Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе «не проседало» при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.







